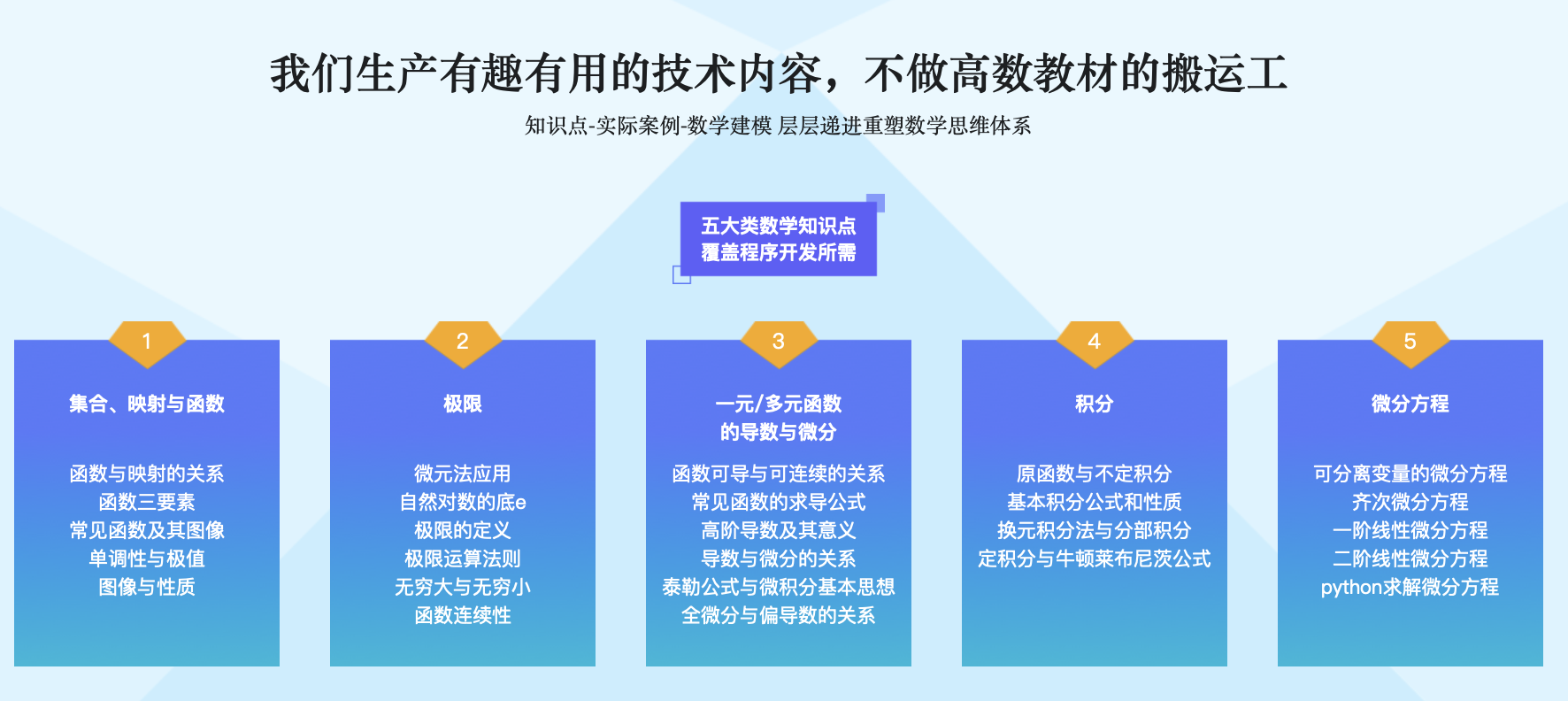
专为程序员设计的高等数学课【已完结 2G】
-
第1章 课程介绍
本章主要整体介绍课程,讲解高等数学与其他学科的结合应用,包含新兴理论算法及其前沿应用。另外,课程许多章节都有实战训练,会使用到python、SPSS或MATLAB等程序语言和应用软件。
- 1-1 课程导学试看
-
第2章 【高数基础】集合、映射与函数
本章讲述的内容会在高中所学概念的基础上作进一步拓展,以便适应高等数学的需求。重点在于了解映射与函数的关系、常见函数图像及性质。
- 2-1 集合的概念
- 2-2 映射的概念
- 2-3 函数的概念
- 2-4 函数的几个特性
- 2-5 常见函数归纳
- 2-6 方程与函数
- 2-7 函数应用举例
-
第3章 极限及应用
对于极限的学习,关键在于对定义的理解,而不是做太多的题目。本章重点从极限产生的背景开始讲解极限的定义、无穷小量以及函数的连续性。
- 3-1 极限产生的背景
- 3-2 极限的定义
- 3-3 无穷小量
- 3-4 极限运算法则
- 3-5 两个重要极限
- 3-6 函数连续性试看
-
第4章 一元函数的导数与微分
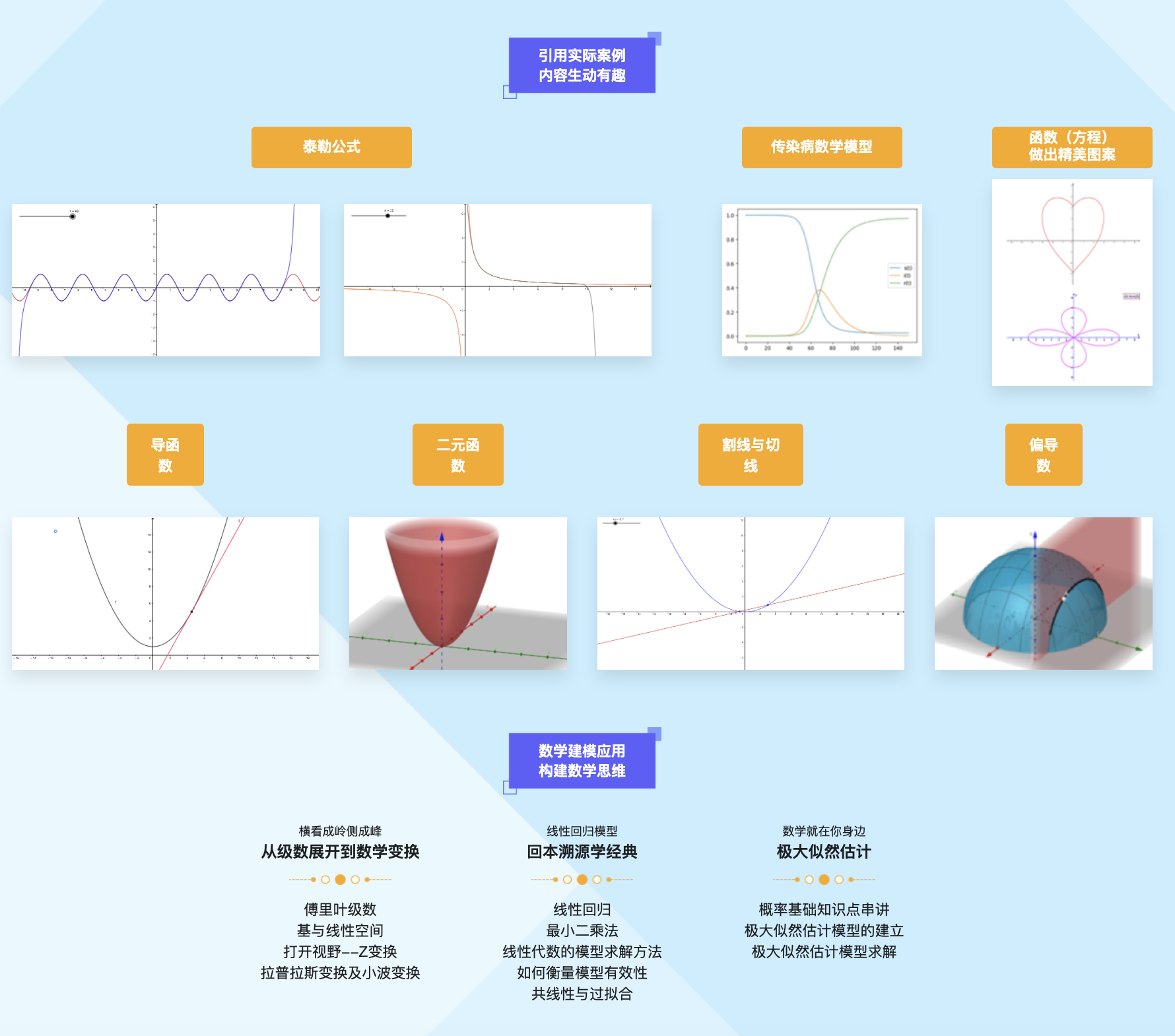
本章首先需要理清导数和微分之间的关系、函数极值点及增减性的求解方法;其次需要尽可能理解微分思维方式,而泰勒公式就是微分思维的体现,理解泰勒公式的本质对于后续算法理解有重要意义。
- 4-1 微积分诞生的背景
- 4-2 理解导数的定义
- 4-3 求导公式
- 4-4 微分中值定理
- 4-5 函数单调性与极值
- 4-6 凹凸性与拐点
- 4-7 洛必达法则
- 4-8 微分的定义
- 4-9 微分应用-近似计算
- 4-10 泰勒公式定义
- 4-11 泰勒展式的收敛域
- 4-12 牛顿迭代法解方程试看
- 4-13 第四章 习题练习
-
第5章 多元函数的导数与微分
本章需要着重理解方向导数与梯度的概念,因为算法的大厦将在此奠基。求多元函数极值在后续两个章节“线性回归模型”和“极大似然估计”中均有重要运用。
- 5-1 空间方程基础知识
- 5-2 二元函数极限的定义
- 5-3 偏导数-
- 5-4 求多元函数极值
- 5-5 全微分
- 5-6 方向导数与梯度下降算法
- 5-7 利用python实现梯度下降算法(上)
- 5-8 利用python实现梯度下降算法(下)
- 5-9 第五章 习题练习
-
第6章 积分定律
积分在物理学和几何学中有及其广泛的直接应用,有明确的物理意义与之对应,同时也是求解微分方程的基础,本章重点在于掌握常用的积分技巧。
- 6-1 不定积分
- 6-2 定积分的定义
- 6-3 牛顿-莱布尼茨公式
- 6-4 定积分应用-求平面曲线的弧长
- 6-5 第六章 习题练习
-
第7章 微分方程
微分方程是描述事物运行规律的利器,除了在物理学领域广泛应用外,也是数学建模的常客,具体应用在后续专门章节介绍。本章主要学习微分方程的求解方法。
- 7-1 微分方程的意义
- 7-2 求几种特定形式的微分方程的通解
- 7-3 利用python求微分方程的通解
- 7-4 微分方程的数值解-欧拉法
- 7-5 利用python实现欧拉法
- 7-6 微分方程的数值解–龙格-库塔法
- 7-7 利用python实现龙格-库塔法
- 7-8 第七章 习题练习
-
第8章 常见微分方程数学建模
本章将让大家感受微分方程数学模型在各行业的实际应用效果,同时让大家了解数学建模的一般方法。
- 8-1 传染病的微分方程模型(上)
- 8-2 传染病的微分方程模型(下)
- 8-3 利用python实现求微分方程组的数值解
-
第9章 线性回归
线性回归模型是多元函数极值最经典的应用之一,也是机器学习最基础的算法,属于统计模型范畴,因其简单有效,应用广泛。本章重点讲解线性回归模型,同时利用SPSS实战,活学活用。
- 9-1 最小二乘法
- 9-2 使用线性代数实现最小二乘法(上)
- 9-3 使用线性代数实现最小二乘法(下)
- 9-4 线性回归的假设与检验
- 9-5 利用SPSS实现线性回归
-
第10章 极大似然估计
在模型已定,参数未知的情况下,利用极大似然估计的方法估计参数会是一个很好的选择。本章介绍极大似然估计的求解主要利用多元函数极值求解方法。
- 10-1 生活中的极大似然估计
- 10-2 连续型随机变量对应的极大似然估计
- 10-3 例题讲解
-
第11章 傅立叶变换
同一个事物,观察角度不一样,得到的结果就不一样,但是事物本身并未变化。比如正弦波函数在时域上看是无限延伸的,但是在频域上看只是一条谱线。本章将带你认识数学变换的本质。
- 11-1 傅里叶变换的意义
- 11-2 补充知识
- 11-3 傅里叶级数
- 11-4 傅里叶变换
-
第12章 课程总结
本章对课程做整体总结并对后续学习给出建议!
- 12-1 课程总结